1.5 KiB
Etude de jeux 3x3 (Et 2 figures présentes par cartes) :
On garde 60 cartes pour un paquet et 1 combinaisons toute les 15 cartes minimum.
Pourquoi 15 ? Car ¼ * 60 Donc 1 carte -> 3 cartes assemblables Soit 15x1 cartes -> 15*3 cartes assemblables On cherche 15 cartes uniques avec du 3x3 (Cartes uniques : attention symétrie)

Possibilité du rond (9) Possibilité du cercle (8) Soit 72(9*8) combinaisons totales
Mais on retire les doublons car cartes uniques :
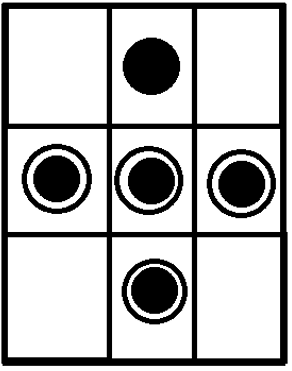
Possibilité du rond (5) Possibilité du cercle (4) Soit 20(5*4) combinaisons totales donc on en retire la moitié afin d’enlever les doublons. Donc 10 cartes doublées. NB : Doublons (Matrice carré) : Si 2 figures sur un axe central.
On prend alors 15 de ces cartes uniques et on cherche 3 combinaisons pour chaque.
Etude de jeux 4x3 :
Pb : comment sont choisies les cartes dans un paquet ?
Les cartes présentes dans le paquet 4x3 :
Nbforme : (carré,rond,ect …) Nbfigure : (nommbre d’éléments sur une carte) | ex classique : 1 cercle et 1 rond sont présents par carte n : nb de type d’éléments (ex avec 3 : Un grand cercle, un cercle moyen, un rond)
36 x (nbfrome^nfigure)xsomme :k=1 :n-1(k)
Soit (jeu classique : nbforme = rond, nfigure=2, n=2) : 361^22=72 cartes uniques Pourquoi :
36 : nombre de cartes uniques :
Cartes uniques : cartes qui peut importe la symétrie n’a pas d’équivalent dans le paquet