|
|
1 year ago | |
|---|---|---|
| src | 1 year ago | |
| .gitignore | 1 year ago | |
| README.md | 1 year ago | |
| all-sorts.png | 1 year ago | |
README.md
📚 Algorithmique et Complexité
Rédigé par @remi.lavergne à l'aide en partie de sources citées ci-dessous.
Snippets de code pour la SAÉ 2.02 mettant en avant:
- L'analyse d'algorithme
- Le calcul de complexité
- La visualisation d'algorithme via des graphes et des arbres
- L'optimisation d'algorithme
🔎 Calcul de la Complexité d'un Algorithme
☝️ Avant toute chose
Je sais que vous avez sûrement envie de commencer à calculer ou faire vos graphiques de temps d'éxecution. Mais avant toute chose, il est essentiel de commencer par se poser.
Le mieux et de se munir d'un papier et d'un crayon pour faire un schéma ou une liste des étapes de l'algorithme.
Cela vous permettra de mieux comprendre le fonctionnement de l'algorithme et de mieux visualiser les boucles et les appels récursifs.
📝 Par exemple, pour la recherche dichotomique, vous pouvez commencer par écrire les étapes de l'algorithme sur papier:
- On commence par initialiser les variables
gaucheetdroiteà 0 etn-1. - On calcule le milieu de la liste.
- On compare la valeur recherchée avec la valeur au milieu de la liste.
- Si la valeur recherchée est plus petite, on met à jour la variable
droiteàmilieu-1. - Sinon, on met à jour la variable
gaucheàmilieu+1. - On répète les étapes 2 à 5 jusqu'à ce que la valeur recherchée soit trouvée ou que
gauchesoit supérieur àdroite.
Comme un diagramme de flux finalement !
👀 Version plus visuelle:
graph TD
A[Initialisation] --> B[Calcul du milieu]
B --> C[Comparaison]
C --> |Valeur trouvée| D[Fin]
C --> |Valeur plus petite| E[Mise à jour de droite]
C --> |Valeur plus grande| F[Mise à jour de gauche]
E --> B
F --> B
Notions de Base
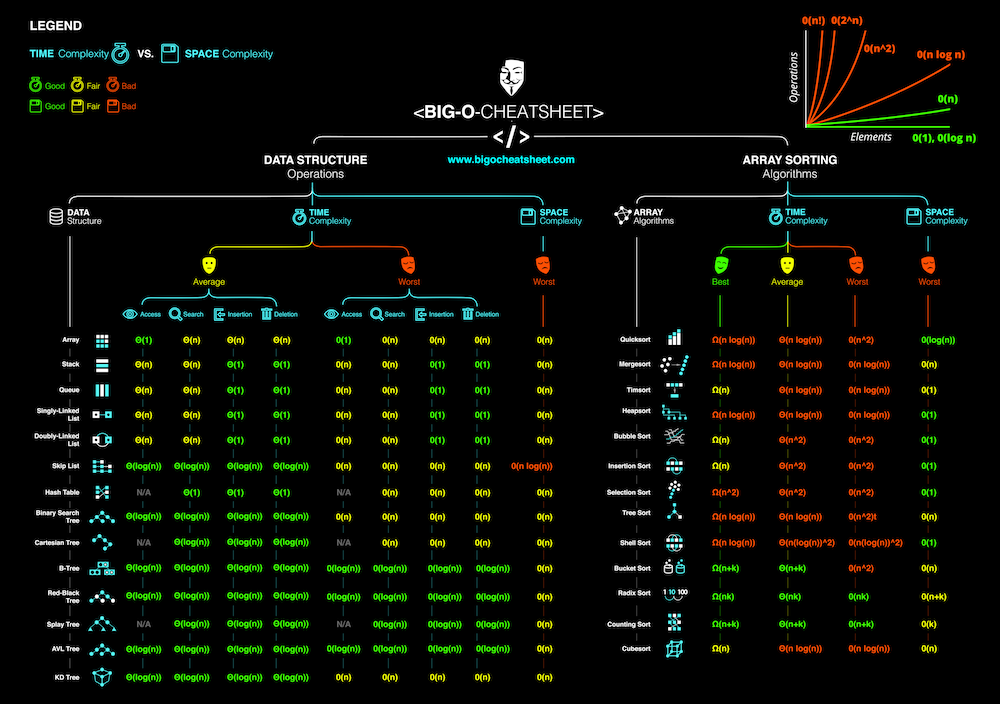
1. Notation Big-O
La notation Big-O est utilisée pour décrire la complexité d'un algorithme. Elle indique comment le temps d'exécution ou l'espace mémoire requis par un algorithme augmente en fonction de la taille de l'entrée. Voici quelques exemples courants de complexités:
- O(1) : Complexité constante. Le temps d'exécution ne dépend pas de la taille de l'entrée.
- O(n) : Complexité linéaire. Le temps d'exécution augmente linéairement avec la taille de l'entrée.
- O(n^2) : Complexité quadratique. Le temps d'exécution augmente quadratiquement avec la taille de l'entrée. Pareil pour O(n^3), O(n^4), etc.
- O(log n) : Complexité logarithmique. Le temps d'exécution augmente logarithmiquement avec la taille de l'entrée.
- O(n log n) : Complexité linéaire-logarithmique. Couramment observée dans les algorithmes de tri efficaces comme le tri par fusion.
Pour ceux qui n'arrivent pas à visualiser la présence du logarithme dans les complexités, voici un exemple simple:
- O(log n) : Supposons que vous ayez une liste de taille 8. Vous pouvez la diviser en deux parties de taille 4, puis en quatre parties de taille 2, puis en huit parties de taille 1. Cela prendra 3 étapes pour atteindre la taille 1. Donc, log(8) = 3. Contrairement à l'exponentiel, le logarithme augmente lentement avec la taille de l'entrée. Et contrairement à O(n), içi on a pu diviser la liste en deux à chaque étape, ce qui est plus efficace.
Ordre d'efficaicté des complexités:
Du plus efficace au moins efficace:
O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(n^3) < O(2^n)
2. Variables d'Intérêt
Les variables d'intérêt pour l'analyse de la complexité sont généralement la taille de l'entrée n et le nombre d'opérations élémentaires effectuées par l'algorithme.
⬇️ Voir juste en dessous ⬇️
3. Instructions Élémentaires
Ce sont des opérations de base, comme l'addition, l'affectation, la comparaison, etc., qui ont un coût constant, noté O(1).
Dans le calcul, on suppose que le coût de chaque instruction élémentaire est le même. Elles ont un réel impact lorsqu'elles sont exécutées un grand nombre de fois, comme dans les boucles (for, while) ou les appels récursifs.
Il peut s'agir des opérateurs d'affectation (=) ou d'opération (+ - * / > >= <= < and or), ainsi que les fonctions natives comme len ou range. Celles-ci compte +1 à chaque apparition.
+0 pour def, for, while, if, else ou return +2 pour les opérateurs comme +=, -=, etc...
Ne pas oublié de prendre en compte si certaines instructions sont incluses dans des boucles !
Calcul de la Complexité
1. Complexité Temporelle
💡Étapes Générales :
- Identifier les boucles : Notez le nombre d'itérations de chaque boucle. (souvent en fonction de n )
- Analyser les récursions : Utilisez les relations de récursion pour déterminer le nombre d'appels récursifs. (En général, on note aussi le nombre d'appels récursifs en fonction de n)
- Calculer la somme : Additionnez le coût des instructions élémentaires pour chaque itération ou appel récursif.
- Combiner les résultats : Pour finir, combinez les coûts pour obtenir la complexité totale.
Exemple : Tri à Bulles
def triBulles(T):
for i in range(len(T)-1, 0, -1): # Boucle extérieure (+2)
for j in range(i): # Boucle intérieure (+1)
if T[j+1] < T[j]: # Comparaison +4 (car 2 accès à un tableau, une comparaison et une addition)
tmp = T[j] # Affectation +2 (un accès et une affectation "=")
T[j] = T[j+1] # Affectation +4 (2 accès, une affectation et une addition)
T[j+1] = tmp # Échange +3 (1 accès, une affectation et une addition)
- La boucle extérieure s'exécute
n-1fois. - La boucle intérieure s'exécute
ifois à chaque itération de la boucle extérieure. - Le coût de la comparaison et de l'échange est constant. On suppose donc que chaque itération de la boucle intérieure coûte
O(1).
La complexité temporelle du tri à bulles est donc O(n^2).
Pourquoi ?
Car la boucle extérieure s'exécute
n-1fois et la boucle intérieure s'exécute en moyennen/2fois, on le sait grâce à l'analyse qu'on a faite avant. Il est en effet essentiel de regarder comment fonctionne l'algorithme pour savoir que le tri à bulles, divise à chaque itération le nombre d'éléments à trier par 2.
En réalité le calcul nous donne: [n(n-1)/2 = (n^2 - n)/2 = O(n^2)] Car on ne garde que le terme dominant. (ici n^2)
Pourquoi ?
Car on ne s'intéresse qu'au terme dominant, c'est-à-dire le terme qui croît le plus rapidement en fonction de la taille de l'entrée. Les autres termes sont négligés car ils deviennent insignifiants lorsque la taille de l'entrée devient grande.
Au final la représentation avec matplotib donne quasiment la même chose:
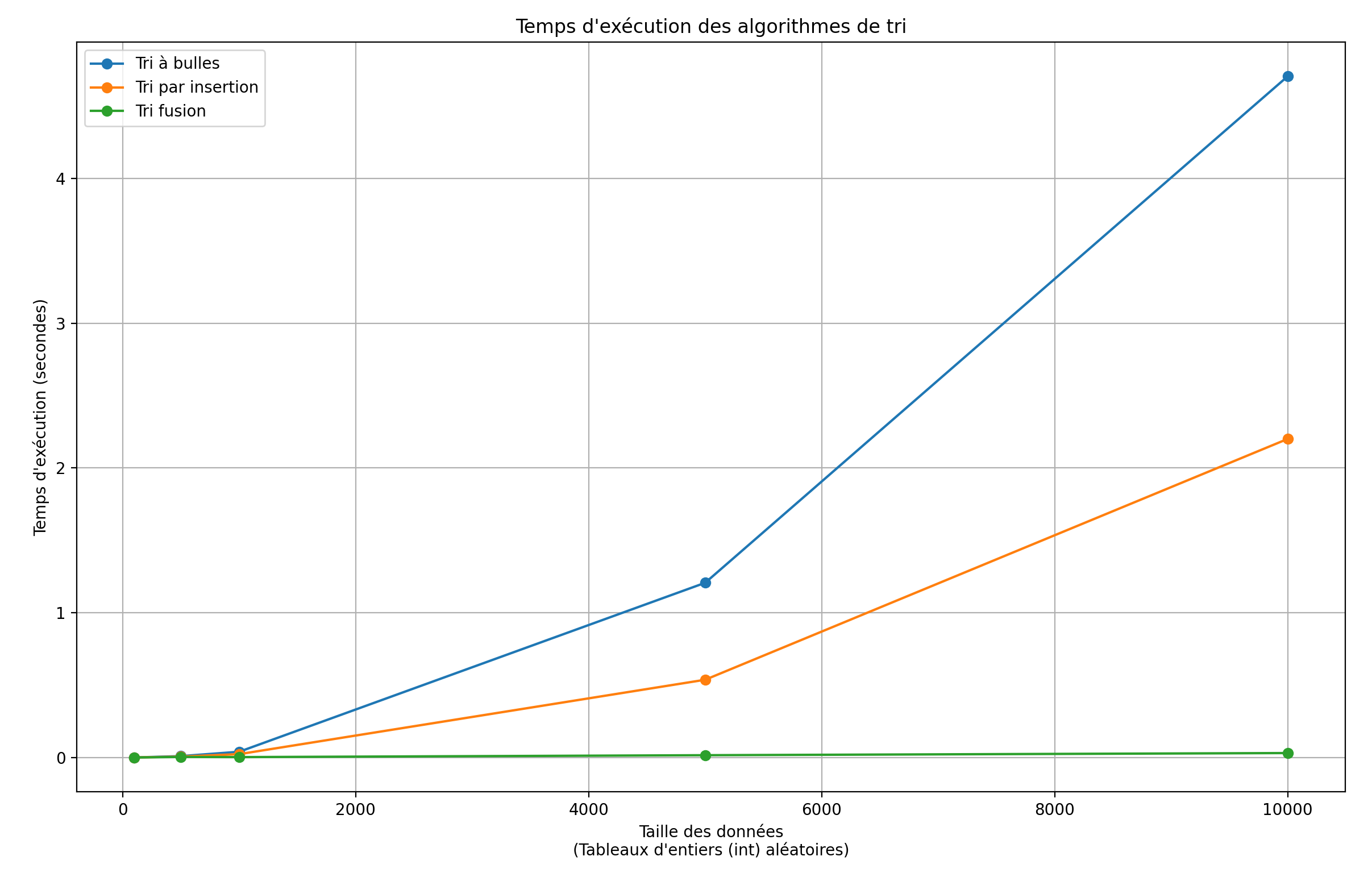
😨 N'ayez pas peur
Au final, l'analyse de la complexité n'est pas si compliquée. Il suffit de suivre les étapes générales et de bien comprendre le fonctionnement de l'algorithme avant dee se lancer dans le calcul.
Lisez et comprenez le fonctionnement de l'algorithme. Ensuite le calcul des coûts ne devient qu'une simple étape de calcul mathématique.
🏎️ Optimisation & factorisation
🚧 En cours de rédaction...